3-1-1
Different plasma creatinine assays and impact on glomerular filtration
rate estimation
MA Ying-Chun, ZUO Li, WANG HaiYan : On behalf of Chinese eGFR Investigation
Collaboration Group
Introduction:
Recently, we modified the Modification of Diet in Renal Disease (MDRD)
equation, which was based on plasma creatinine (Pcr) by Jaffe's kinetic
method, for Chinese patients with chronic kidney disease (CKD). The aim
of the present study was to rewrite the equation based on Pcr by the of
enzymatic method, and make sure the performance of the rewritten equation
was equivalent with the published one.
Methods:
All plasma samples were measured in a single laboratory (Department of
Laboratory, Peking University First Hospital) using two different methods,
both on a Hitachi 7600 auto-analyzer: Jaffeユs kinetic method ( Pcr-Jaffe),
reagents were from Roche Diagnostics, normal reference range 0.72-1.48mg/dL;
and enzymatic wet chemistry method (Pcr-enzyme), reagents were from Kyowa,
normal reference range 0.24-1.17mg/L. The between-day coefficients of
variances were both <5.0% at Pcr concentrations of 6.0mg/L and 1.0mg/L
during the study period.
The dual plasma sampling 99mTc-DTPA plasma clearance was used as reference
glomerular filtration rate (GFR).
First, Pcr-Jaffe was put into the modified MDRD equation to estimate
GFR:
eGFR1 = 206_Pcr-Jaffe -1.234 _Age-0.227 (Female_0.80) Equation-1
Second, Pcr-enzyme was also directly put into the equation-1, to calculate
eGFR2.
Third, a new equation based on Pcr-enzyme was developed by the log transformed
multiple stepwise regression method.
Fourth, the difference and accuracy of the new equation based on Pcr-enzyme
were compared with the equation-1.
Results:
The new equation based on Pcr-enzyme was constructed from a random sample
of 372 patients out of the 555 patients.
eGFR3 = 170_Pcr-enzyme -0.996 _Age-0.244 (Female_0.81) Equation-2
Where: GFR was in unit of ml/min/1.73m2, Pcr was in unit of mg/dL, Age
was in unit of years
Equation-2 had similar difference and accuracy compared with equation-1.
But if Pcr-enzyme was used in equation-1 or Pcr-Jaffe was used in equation-2,
higher bias and lower accuracy were resulted in separate CKD stages.
Conclusion:
Different Pcr methods have great influence on the estimated GFR., When
estimate GFR, one should know the Pcr method, and select the corresponding
equation. Before a creatinine standardization program is adopted, as a
temporary solution, we suggest that laboratories, practitioners and nephrologists
select the right equation according what method for Pcr they use.
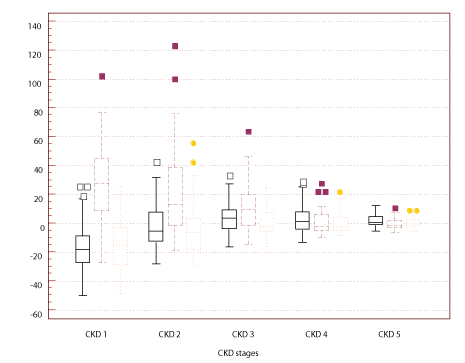
Figure 1 Box-and-whisker plots showing the 25th, 50th and 75th percentiles of difference between eGFR and rGFR in difference stages of CKD. Solid lines represent the results of eGFR1; dashed lines represent the results of eGFR2; dotted lines represent the results of eGFR3. Outliers and extremes are also shown.
3-1-22
How to Select the Appropriate Glomerular Filtration Rate Estimating Equation?
(to be published in Hong Kong Journal of Nephrology)
Li Zuo, M.D.; Hai-Yan Wang, M.D.
Institute of Nephrology, Peking University First Hospital
For decades, efforts had been made to improve the accuracy of plasma
creatinine (Pcr) based glomerular filtration rate (GFR) estimating equations,
and many different equations had been published (Table 1). Before the
publication of Modification of Diet in Renal Disease (MDRD) study equation,
the GFR estimating equation mainly used in mainland China was the Cockcroft-Gault
(C-G) equation(1). In 1999, Levey et al. published the MDRD equations(2).
In 2000, the authors simplified the MDRD equation(3). In 2006, the MDRD
equations was re-expressed(4). I; in the same year, Ma et al. modified
the MDRD equation for Chinese patients with chronic kidney disease (CKD)(
5).
There are so many options, - which GFR estimating equation should we use,
especially in Chinese patients with CKD? In this review, methods to compare
different equations will be discussed; the importance of calibration of
Pcr will be emphasized; and some tricky issues about development of these
equations will be presented which should be helpful in aiding our selection
from these flying equations.
1. The C-G equation and the abbreviated MDRD equation
These equations are mostly used in Mainland China. There are several limitations
to the C-G equation. _ The reference GFR was the 24-hour-urine creatinine
clearance (Ccr), so the predicted value of C-G equation is actually Ccr
in units of ml/min; _ The sample size was 236, and all of them were male.
In the discussion section, the authors suggested that "Various authors
have recommended reducing the predicted Ccr by 10-20% (for female). A
15% reduction appears appropriate." (1). The MDRD equations seem
a great improvement. The renal clearance of 125I-iothalamate was used
as reference GFR in equations development, and the sample size was relatively
large.
It is thus expected that MDRD equations should give a more accurate estimated
GFR (eGFR). But these equations significantly underestimate GFR when the
real value is in the near-normal range(6- 11), and overestimate GFR in
advanced kidney failure(10, 11). This phenomenon exists not only in Whites
and African-American, but also in other racial groups. We also found this
trend in Chinese patients with CKD(10), and by adding a racial factor
for Chinese to the MDRD equation, the unpleasant trend was significantly
reduced(5), but still exists. This is partly due to the problem of regression.
2. Problem of Regression in GFR equation development
There is no physiological basis for GFR equations;; they are just empirical
statistical regression equations. When we fit a regression model, it means
that you tell the model メI think these variables can predict GFR, do it
for meモ. The software then does the model fitting as you commanded, and
tells you how well the model fitting is. Usually, GFR can not be wholly
explained by the dependent variables, this is partly due to the random
error in measurement of dependent variables and reference GFR, and partly
due to the fact that メnot all dependent variables are included in the
modelモ. This is to say that the model can not reflect the real world perfectly
as it is. There are several factors that may influence the accuracy of
eGFR.
(1) Reference GFR. Until now the renal clearance or plasma clearance of
inulin has been considered the best estimate of GFR. Other reference GFR
methods include clearance of Diethylene triamine pentaacetic acid (DTPA),
ethylenediaminetetraacetic acid (EDTA), etc. however , no reference method
can give results without some error. The Diurnal variation of GFR can
be as large as 10-20%(12- 14), and Pcr can not reflect this acute daily
variation. Furthermore, there are systematic differences between different
reference GFR methods. For example, studies have shown that results of
DTPA plasma clearance by the dual plasma sampling method overestimates
GFR by an average of 0.5 mL/min when GFR = 10 mL/min, and underestimates
GFR by an average of 20 mL/min when GFR = 100 mL/min)( 15). Renal clearance
of iothalamate, used as the standard measure of GFR in the MDRD study,
It overestimates renal clearance of inulin by 3 to 5 mL/min at low levels
of GFR and by 15 to 25 mL/min in healthy subjects(16, 17). When we fit
the models, we actually request the computer to predict DPTA plasma clearance
or iothalamate renal clearance;, not the メrealモ GFR. The systemic difference
between reference GFR methods will definitely result in different GFR
predicting equations.
(2) Plasma Pcr can be measured using different method, such as kinetic
Jaffeユs method, enzyme method, etc. Each method can be performed in different
auto-analyzers. This will induce intra-laboratory variation. For example,
for the same plasma samples, the Pcr values reported by MDRD study (Beckman
Astra CX3 autoanalyzer (Brea, CA)) are 0.23mg/dL lower than values reported
by the National Health and Nutrition Examination (NHANES) III (Hitachi
737 analyzer (Boehringer Mannheim Corp, Indianapolis, IN))( 18), although
both of them used the modified kinetic Jaffe reaction method to measure
Pcr. If the MDRD plasma samples would be measured in a third laboratory,
and the Pcr be 5% systemically higher than MDRD value, then the coefficient
of 186 in abbreviated MDRD equation would change to [186_(-1.154)_ln(1/1.05)=]196;
and if Pcr be 5% systemically low, it would change to [186_(-1.154)_ln(1/0.95)=]175.
Very recently, Levey et al. calibrated the Beckman assay used in MDRD
study to the Roche/Hitachi P module Creatinase Plus enzymatic assay (Roche
Diagnostics, Basel, Switzerland), which was traceable to an isotope-dilution
mass spectrometry assay at the National Institute of Standards and Technology(19).
By doing so, the coefficient of abbreviated MDRD equation was changed
from 186 to 175(4). Clearly, different Pcr method will result in different
eGFR estimating equation.
(3) A big problem in eGFR equation development is that the regression
model can not reflect the real world. Both the MDRD study and Maユs study
assumed that log transformed Pcr will be linearly related with real GFR.
Although this is nowadays the best model to describe the relationship
between Pcr and GFR, it is in fact not the real world. As we know, because
of the tubular secretion of creatinine, Pcr will not increase in early
stages of GFR decrease, so the model will relate an apparently normal
Pcr with a decreased GFR, and fit the data to output an eGFR equation.
When this equation is used in normal individuals who have normal Pcr value
and normal real GFR, the eGFR will definitely lower than the real value.
Another problem is that the model will strictly obey your command to keep
the linear relationship between log transformed Pcr and log transformed
real GFR although sometimes it is not real, so when GFR is relatively
normal, a small change in Pcr will result in great change in eGFR, which
is impossible. As an example: Imagine, a 40 year old White male with chronic
kidney disease., 2 weeks ago his Pcr value was 0.55 mg/dL. Using the abbreviated
MDRD equation, his eGFR would have been 175 ml/min/1.73m2
then. He came to visit his doctor today., Pcr was 0.60 mg/dL, his eGFR
value is now 159 ml/min/1.73m2 . The difference
between Pcr was only 0.05mg/dL, which might be due to laboratory variation,
but the resultant eGFR difference was as large as 16 ml/min/1.73m2.
3. Comparing different GFR estimating methods
To decide which method is better than the other , or whether these two
methods are equivalent, we need to make some comparison. Correlation should
not be used to describe agreement between methods. This is because the
fact that highly correlated methods still have the possibility to be systemically
different from each other. This issue has been discussed by Bland JM and
Altman DG(20). Regressing one method against another method should also
be avoided. Two equivalent methods will be erroneously judged not equivalent
by regression, this phenomenon is called "regression toward the mean
(RTM)".
The phenomenon of RTM will be shown here by an example. Suppose we have
300 subjects:, the mean real GFR is 60 ml/min/1.73m2,
the standard deviation is 20 ml/min/1.73m2. For each subject, eGFR is
estimated using a given method with normal distributed random error.,
Suppose the standard deviation for each subject is 15% of the real GFR,
we will call this eGFR1. eGFR is measured again using the same method
with the same standard deviation, we call this eGFR2. eGFR1 and eGFR2
are equivalent to each other apart from the random error. If we regress
eGFR2 against eGFR1 (Figure 1 left panel), the intercept will be 10.68ア2.02
(significantly different from 0, P<0.0001), and the slope will be 0.83ア0.03
(significantly different from 1, P<0.0001) in this simulation. This
result misleadingly concludes that there is a systemic difference between
eGFR2 and eGFR1. This is not a coincidence: If eGFR1 is regressed against
eGFR2, the slope is again greater than 0 and the slope is again less than
1 (Figure 1 right panel). So, when we compare two methods, we can not
simply regress one against the other. The proper method to compare eGFR1
and eGFR2 is a Bland-Altman plot(20). In a Bland-Altman plot, the difference
between eGFR2 and eGFR1 is regressed against the average of them, the
95% confidence interval of difference is also shown (Figure 2 left panel).
It clearly shows that eGFR1 and eGFR2 perfectly agree with each other
(the average difference is 0.04ア12.85 ml/min/1.73m2).
When comparing different methods, many authors (including our paper published
in Am J Kidney Dis(10)) expand the Bland-Altman plot by regressing difference
against average, and claim that if the slope is not equal to zero then
the difference is proportional to average. The fact is that the slope
can also be caused by different size of intra-subject variance between
methods. We will use the same 300 subjects as before with a mean real
GFR of 60 ml/min/1.73m2, and standard deviation
of 20 ml/min/1.73m2 to illustrate why. Suppose the
above real GFR is estimated by method 1 and method 2 with a normal distributed
random error, and the intra subject standard deviation for these two methods
is 15% and 7% of real GFR respectively. There is no significant difference
between two methods using paired t-test. The Bland-Altman regression looks
like the right-hand panel in figure 2. The slope is -0.10ア0.03 (significantly
different from 0, P<0.001), the intercept is 4.06ア1.24 ml/min/1.73m2
(significantly different from 0, P=0.002) in this simulation. The real
world is that there is no systemic difference between method 1 and method
2, the slope and intercept should both be zero.
The slope is useful when two methods are compared with a certain reference
method. By comparing method 1 with the reference and comparing method
2 with the reference, we get two Bland-Altman regression slopes. The method
with near-zero slope is expected to be better than the other one (mean
difference and its 95% confidence interval should also be considered).
In our previous work, the performance of the MDRD equation in Chinese
patients with CKD was evaluated, difference between MDRD equation estimated
GFR and reference GFR was regressed against their mean, the slope was
significantly less than zero., We concluded that the MDRD equation underestimates
reference GFR when real GFR was near-normal (10)., Iin the discussion
section, we should have mention the possibility of different error size
between the MDRD equation and the reference GFR method that could cause
the none zero slope. This is a shortcoming. Recently, using the same dataset,
we modified MDRD equation(5). In this study, the modified MDRD equation
and original MDRD equation were compared with reference method. It was
shown that the slopes of Bland-Altman regressions for the modified equations
were much closer to zero than that of the original equations, which means
that the modified equation performs better. But the slope was still none-zero,
we did not know which condition caused this none-zero slope -, the difference
of error size of method, the real trend of difference along average, or
the regression problem mentioned in section 2.
4. Importance of calibration for creatinine method
Creatinine calibration is a big issue in GFR estimation. If Pcr is systemically
high or low, the eGFR will dramatically shift away from the real eGFR
value. A lot of authors have emphasized the importance of calibration
of creatinine(4, 18, 21- 24). Letユs run a simulation. Suppose we have
a group of 1000 male subjects, they are all of the age of 40, and their
Pcr are 0.30, 0.31, 0.32ノ 15.00 mg/dL respectively, We calculate eGFR
for each of them using the abbreviated MDRD equation, and plot eGFR against
Pcr (the solid curve in figure 3); the upper and lower dashed curve represent
deviated eGFR if Pcr was 5% low or high. It is clear that a small change
of creatinine causes eGFR significantly deviating from its real value.
5. Equation selection and result explanations
With Pcr in hand, you need to select one of the Pcr based equations to
estimate eGFR. Several factors will influence your selection, such as
race and method of creatinine. You are advised to select the equation
specific for a certain racial group, and which uses the same creatinine
method as yours.
It is a good idea to send your plasma specimens to the laboratory that
developed the equations to have the Pcr measured. But it is cumbersome
and also impossible for all the renal centers to do so. The re-expressed
MDRD equations used the standardized creatinine method(4). Any renal centers
can have their creatinine value be calibrated to the standardized creatinine
value without the need to send their specimens to the laboratory where
MDRD study measured their creatinine.
If the eGFR equation is used for survey study, the Pcr method should be
calibrated, otherwise, the estimated prevalence or incidence will significantly
deviate from their real value. For out-patients practice, although systemically
biased Pcr will result in systemically biased eGFR, it is still useful
to estimate the trend of eGFR over time. If the absolute value of eGFR
is not importance to you, and your interest is the eGFR trend, an un-calibrated
Pcr does no harm.
Table 1. Plasma creatinine based equations
Author (year) (reference) |
Equation |
| Jelliffe (1971) ( 25) |
 |
| Mawer (1972) ( 26) |
 |
| Jelliffe (1973) ( 27) |
|
| Cockcroft-Gault (1976) (1) |
|
| Hull (1981) ( 28) |
|
| Bjornsson (1983) ( 29) |
 |
| Gates (1985) ( 30) |
|
| Levey (1999) ( 2) |
|
| Levey (2000) ( 3) |
 Figure
1. Artifact that two methods are not equivalent
when they are actually equivalent. Left panel: regressing method
2 against method 1. Right panel: regressing method 1 against method 2.
The dashed line is the identical line; the solid line is the regression
line.
Figure
1. Artifact that two methods are not equivalent
when they are actually equivalent. Left panel: regressing method
2 against method 1. Right panel: regressing method 1 against method 2.
The dashed line is the identical line; the solid line is the regression
line.
 Figure
2. Bland-Altman plot.
Figure
2. Bland-Altman plot.
Left panel: a typical Bland-Altman plot. The intra-subject variances are
equal between two methods. Right panel: Bland-Altman plot when the intra-subject
variances are unequal between two methods.
 Figure
3. Importance of calibration of creatinine measurement.
Figure
3. Importance of calibration of creatinine measurement.
The solid curve shows the real creatinine, the curve shift upward if creatinine
is systemically low and shift downward if creatinine is systemically high.
For a 40-year-old White male, if real creatinine =1mg/dL, his eGFR is
88ml/min/1.73m2. If creatinine changes 5% within
the real value (0.95~1.05 mg/dL), the corresponding eGFR will change from
79 to 100 ml/min/1.73m2; if the real creatinine
is 2mg/dL, ア5% change of creatinine (1.9~2.1 mg/dL) will cause eGFR varying
from 35 to 45 ml/min/1.73m2.
Reference
- Cockcroft DW, Gault MH.Prediction of creatinine clearance from serum creatinine.Nephron1976;16:31-41
- Levey AS, Bosch JP, Lewis JB, Greene T, Rogers N, Roth D.A more accurate method to estimate glomerular filtration rate from serum creatinine: a new prediction equation. Modification of Diet in Renal Disease Study Group.Ann Intern Med1999;130:461-70
- Levey AS, Greene T, Kusek J, Beck GJ, Group MS.A simplified equation to predict glomerular filtration rate from serum creatinine.J Am Soc Nephrol2000;11:828A (Abstr)
- Levey AS, Coresh J, Greene T et al.Using standardized serum creatinine values in the modification of diet in renal disease study equation for estimating glomerular filtration rate.Ann Intern Med2006;145:247-54
- Ma YC, Zuo L, Chen JH et al.Modified glomerular filtration rate estimating equation for Chinese patients with chronic kidney disease.J Am Soc Nephrol2006;17:2937-44
- Rule AD, Larson TS, Bergstralh EJ, Slezak JM, Jacobsen SJ, Cosio FG.Using serum creatinine to estimate glomerular filtration rate: accuracy in good health and in chronic kidney disease.Ann Intern Med2004;141:929-37
- Rule AD, Gussak HM, Pond GR et al.Measured and estimated GFR in healthy potential kidney donors.Am J Kidney Dis2004;43:112-9
- Verhave JC, Fesler P, Ribstein J, du Cailar G, Mimran A.Estimation of renal function in subjects with normal serum creatinine levels: influence of age and body mass index.Am J Kidney Dis2005;46:233-41
- Lhotta K.Performance of GFR formulas in individuals with normal renal function.Am J Kidney Dis2004;44:939; author reply 939-40
- Zuo L, Ma YC, Zhou YH, Wang M, Xu GB, Wang HY.Application of GFR-estimating equations in Chinese patients with chronic kidney disease.Am J Kidney Dis2005;45:463-72
- Hallan S, Asberg A, Lindberg M, Johnsen H.Validation of the Modification of Diet in Renal Disease formula for estimating GFR with special emphasis on calibration of the serum creatinine assay.Am J Kidney Dis2004;44:84-93
- Hansen HP, Hovind P, Jensen BR, Parving HH.Diurnal variations of glomerular filtration rate and albuminuria in diabetic nephropathy.Kidney Int2002;61:163-8
- SIROTA JH, BALDWIN DS, VILLARREAL H.Diurnal variations of renal function in man.J Clin Invest1950;29:187-92
- WESSON LG Jr, LAULER DP.Diurnal cycle of glomerular filtration rate and sodium and chloride excretion during responses to altered salt and water balance in man.J Clin Invest1961;40:1967-77
- Waller DG, Keast CM, Fleming JS, Ackery DM.Measurement of glomerular filtration rate with technetium-99m DTPA: comparison of plasma clearance techniques.J Nucl Med1987;28:372-7
- Odlind B, Hallgren R, Sohtell M, Lindstrom B.Is 125I iothalamate an ideal marker for glomerular filtration?.Kidney Int1985;27:9-16
- Perrone RD, Steinman TI, Beck GJ et al.Utility of radioisotopic filtration markers in chronic renal insufficiency: simultaneous comparison of 125I-iothalamate, 169Yb-DTPA, 99mTc-DTPA, and inulin. The Modification of Diet in Renal Disease Study.Am J Kidney Dis1990;16:224-35
- Coresh J, Astor BC, McQuillan G et al.Calibration and random variation of the serum creatinine assay as critical elements of using equations to estimate glomerular filtration rate.Am J Kidney Dis2002;39:920-9
- Junge W, Wilke B, Halabi A, Klein G.Determination of reference intervals for serum creatinine, creatinine excretion and creatinine clearance with an enzymatic and a modified Jaffe method.Clin Chim Acta2004;344:137-48
- Bland JM, Altman DG.Statistical methods for assessing agreement between two methods of clinical measurement.Lancet1986;1:307-10
- Murthy K, Stevens LA, Stark PC, Levey AS.Variation in the serum creatinine assay calibration: a practical application to glomerular filtration rate estimation.Kidney Int2005;68:1884-7
- Coresh J, Eknoyan G, Levey AS.Estimating the prevalence of low glomerular filtration rate requires attention to the creatinine assay calibration.J Am Soc Nephrol2002;13:2811-2; author reply 2812-6
- Stevens LA, Coresh J, Greene T, Levey AS.Assessing kidney function--measured and estimated glomerular filtration rate.N Engl J Med2006;354:2473-83
- Myers GL, Miller WG, Coresh J et al.Recommendations for improving serum creatinine measurement: a report from the Laboratory Working Group of the National Kidney Disease Education Program.Clin Chem2006;52:5-18
- Jelliffe RW, Jelliffe SM.Estimation of creatinine clearance from changing serum-creatinine levels.Lancet1971;2:710
- Mawer GE, Lucas SB, Knowles BR, Stirland RM.Computer-assisted prescribing of kanamycin for patients with renal insufficiency.Lancet1972;1:12-5
- Jelliffe RW.Letter: Creatinine clearance: bedside estimate.Ann Intern Med1973;79:604-5
- Hull JH, Hak LJ, Koch GG, Wargin WA, Chi SL, Mattocks AM.Influence of range of renal function and liver disease on predictability of creatinine clearance.Clin Pharmacol Ther1981;29:516-21
- Mawer GE, Lucas SB, McGough JG.Nomogram for kanamycin dosage.Lancet1972;2:45
- Gates GF.Creatinine clearance estimation from serum creatinine values: an analysis of three mathematical models of glomerular function.Am J Kidney Dis1985;5:199-205